There's real numbers, hyper-real numbers, and surreal numbers.
The question is how we deal with SCALE.
Calculus has the concept of an "infinitesimal", which means a number so small that it's smaller than the smallest real number.
And, it has the concept of "infinity", a number so big it's off the charts.
Unfortunately, calculus is not very precise. It confuses people by mistakenly equating infinities with singularities, and it calls division by zero an "infinity" which is completely wrong.
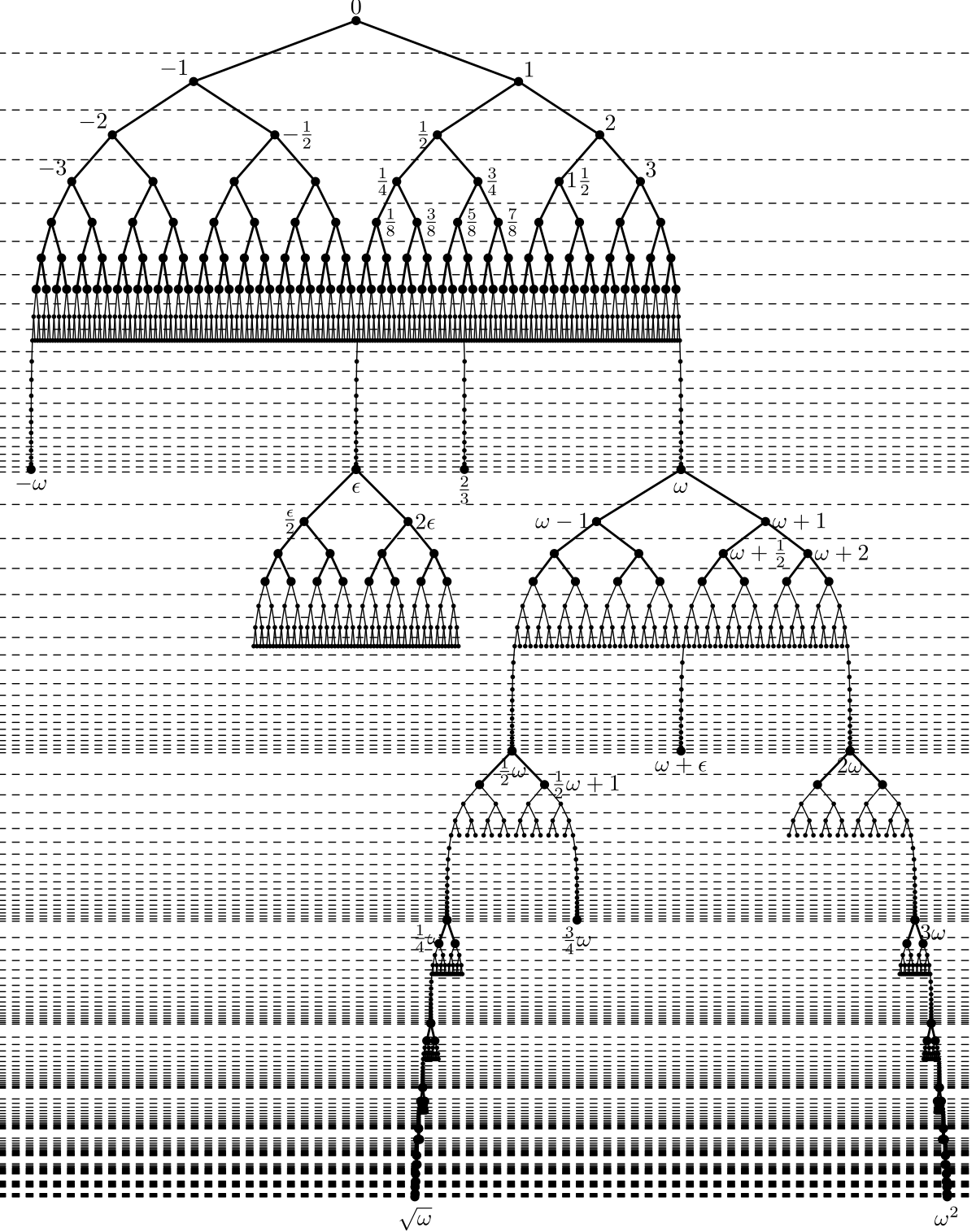
To address these woeful misrepresentations, the mathematicians Georg Cantor and John von Neumann developed "surreal" sets. This is what a surreal number tree looks like:

It contains both infinities and infinitesimals.
There is a "halfway" concept called "hyper-real", which adds an infinity and an infinitesimal to the real number line. But the full implementation allows for the description of things that are smaller than an infinitesimal, and bigger than an infinity.
 en.wikipedia.org
en.wikipedia.org
Why does this matter?
It matters because of topology, which means physics. For example:
The physicists and mathematicians who developed general relativity around the turn of the 20th century, were forced to grapple with preservation of measure. In the specific case of relativity this means things like dot products, and norms. The Lorentz transformations provide an example.
A relativistic "norm" is a distance in spacetime. The rules say this distance has to be the same for all observers, which means the norm has to be preserved through any kind of geometric transformation, including rotations, reflections, translations, and so on.
But the norm, is what they call a quadratic "form", for example in ordinary Euclidean geometry it would be sqrt(x^2 + y^2). So how can we preserve this in the case where x and y are infinitesimals, which means numbers that aren't even on the real number line?
The answer required a deep dive into set theory. In sets, a fundamental concept is the uniqueness of elements. To establish uniqueness, you label, and you count. You take each element and you assign a number to it, it's called an ordinal. You say, this is the first element, that's the second, and so on - and you keep labeling till you get to the end, till you've exhausted all the elements. Then you ask "how many" elements there are, which is the "size" of the set, that's called the cardinal. If you use the real number line for labels, starting with 0, the cardinal (size) becomes the smallest unused number after you're done labeling. Very easy.
What Cantor and von Neumann showed, is there is a way to formalize infinities in a countable manner, which resolves a paradox in the usual Zermelo-Frankel approach they teach in college. The full formal set is called NBG, instead of ZF/C. It stands for Neumann-Bernays-Godel. It requires "sur"-real numbers, so you can count tiny things and huge things. The benefit of NBG is it's fully axiomatizable, whereas ZF/C is not.
 en.wikipedia.org
en.wikipedia.org
NBG let's you make intelligent statements about infinities and infinitesimals, and in some cases even let's you describe singularities. It is the foundation of much of modern mathematics, including group theory which links algebra and geometry through algebraic topology. It provides axiomatic "ordering" of sets, without which we couldn't calculate the distance between points, which means important concepts like area and volume become useless, and induction becomes impossible.
The question is how we deal with SCALE.
Calculus has the concept of an "infinitesimal", which means a number so small that it's smaller than the smallest real number.
And, it has the concept of "infinity", a number so big it's off the charts.
Unfortunately, calculus is not very precise. It confuses people by mistakenly equating infinities with singularities, and it calls division by zero an "infinity" which is completely wrong.
To address these woeful misrepresentations, the mathematicians Georg Cantor and John von Neumann developed "surreal" sets. This is what a surreal number tree looks like:
It contains both infinities and infinitesimals.
There is a "halfway" concept called "hyper-real", which adds an infinity and an infinitesimal to the real number line. But the full implementation allows for the description of things that are smaller than an infinitesimal, and bigger than an infinity.

Surreal number - Wikipedia
Why does this matter?
It matters because of topology, which means physics. For example:
The physicists and mathematicians who developed general relativity around the turn of the 20th century, were forced to grapple with preservation of measure. In the specific case of relativity this means things like dot products, and norms. The Lorentz transformations provide an example.
A relativistic "norm" is a distance in spacetime. The rules say this distance has to be the same for all observers, which means the norm has to be preserved through any kind of geometric transformation, including rotations, reflections, translations, and so on.
But the norm, is what they call a quadratic "form", for example in ordinary Euclidean geometry it would be sqrt(x^2 + y^2). So how can we preserve this in the case where x and y are infinitesimals, which means numbers that aren't even on the real number line?
The answer required a deep dive into set theory. In sets, a fundamental concept is the uniqueness of elements. To establish uniqueness, you label, and you count. You take each element and you assign a number to it, it's called an ordinal. You say, this is the first element, that's the second, and so on - and you keep labeling till you get to the end, till you've exhausted all the elements. Then you ask "how many" elements there are, which is the "size" of the set, that's called the cardinal. If you use the real number line for labels, starting with 0, the cardinal (size) becomes the smallest unused number after you're done labeling. Very easy.
What Cantor and von Neumann showed, is there is a way to formalize infinities in a countable manner, which resolves a paradox in the usual Zermelo-Frankel approach they teach in college. The full formal set is called NBG, instead of ZF/C. It stands for Neumann-Bernays-Godel. It requires "sur"-real numbers, so you can count tiny things and huge things. The benefit of NBG is it's fully axiomatizable, whereas ZF/C is not.
Von Neumann–Bernays–Gödel set theory - Wikipedia
NBG let's you make intelligent statements about infinities and infinitesimals, and in some cases even let's you describe singularities. It is the foundation of much of modern mathematics, including group theory which links algebra and geometry through algebraic topology. It provides axiomatic "ordering" of sets, without which we couldn't calculate the distance between points, which means important concepts like area and volume become useless, and induction becomes impossible.